Die serienmäßige Zündung des Barkas ist an sich eine sehr simple Konstruktion – eine einfache Batterie-Spulenzündung mit Unterbrechersteuerung und ohne Zündverteiler; das ganze mal drei, also für jeden Zylinder eine von den anderen unabhängige Zündanlage – wobei die drei Unterbrecher in einem gemeinsamen Gehäuse zusammengefasst sind und von einer gemeinsamen Nocke betätigt werden. – Entscheidenden Einfluss haben aber die Zündspulen. Forenuser "bic" hat hier umfassend alles Wissenswerte zusammengetragen. 

"Der Grund, warum ich mal also vor einiger Zeit einmal näher mit Zündspulen im Allgemeinen befasst hatte, war mein damals neuer, auf 9,4:1 verdichteter Motor. Denn mit diesem hatte ich mir ein Problem eingehandelt - der Motor neigt in Betriebsbereichen mit (sehr) geringer Last zum Viertakten, also zu Zündaussetzern. Anfangs glaubte ich an den hierfür üblichen Grund, also an eine Überfettung; aber dieser Gedanke erwies sich als nicht haltbar, dies war so nicht zu messen – und ganz im Gegenteil, mit zunehmender Anfettung verringerte sich das Problem sogar ein wenig.

Die Ursache musste daher woanders zu suchen sein; und im "Handbuch Verbrennungsmotor" von Richard van Basshuysen und Fred Schäfer fand ich dann den einen ersten entscheidenden Hinweis: "Ein hoher Abgasanteil im Zylinder führt in der Teillast und besonders im Leerlauf zu drastisch verschlechterten Entflammungsbedingungen". Hierauf hätte ich damals allerdings auch selbst kommen können, denn es ist ja bekannt, dass beim Ladungswechsel unseren Zweitakter nur so viel Abgas aus dem Zylinder verdrängt wird, wie Frischgas hinein gelangt. Und dies ist im Leerlauf und bei niedriger Last wegen der nahezu geschlossenen Drosselklappe herzlich wenig.

Den zweiten Hinweis fand ich dann, als ich in einer Untersuchung zu Zündkondensatoren über das "Paschen-Gesetz" las, wonach man davon ausgehen könne, dass die für die Entstehung eines Zündfunkens erforderliche Zündspannung in etwa proportional zum Verdichtungsdruck steigt und bei einer Verdichtung von 10:1 und 0,6mm Elektrodenabstand schon knapp 20 kV benötigt werden.

Ich konnte also dann davon ausgehen, dass mein Problem tatsächlich von der erhöhten Verdichtung herrührte und meine bis dahin tadellos funktionierende Zündanlage (Ungarnzündung + Beru ZS220) nicht mehr in der Lage war, das bisschen im Zylinder befindliche Gemisch bei Betriebsbereichen mit geringer Last und einer Verdichtung von 9,4:1 sicher zu entzünden bzw. für ein gutes Durchbrennen zu sorgen.

Also musste eine Zündanlage her, die dadurch für Abhilfe sorgt, dass sie eine höhere Zündspannung bereit stellt, damit auch bei einer erhöhten Verdichtung sicher ein Zündfunken zustande kommt. Nur leider ist es damit nicht getan, wie ich bei meiner weiteren Recherche lernen durfte. Für eine sichere Entzündung und ein sicheres Durchbrennen des Gemischs ist nämlich nicht ausschließlich der von der Höhe der Zündspannung abhängige sogenannte Durchbruch (die Entstehung des Plasmakanals zwischen den Kerzenelektroden durch Ionisation) verantwortlich, sondern auch die Dauer der sich daran anschließenden sogenannten "Glimmentladung":

1 = Durchbruch
2 = Glimmentladung

Die Dauer der Glimmentladung ist dann jedoch nicht so sehr von der Höhe der Sekundärzündspannung (die Höhe der Spannung beträgt hier sodann nur noch ca. 1kV), sondern vor allem von der Menge der in der Zündspule gespeicherten Energie abhängig. Daher brauche ich nun eine Zündanlage, welche mir nicht nur in allen Betriebsbereichen sicher mindestens 20 kV zur Verfügung stellt, sondern auch möglichst viel Energie in den Zündspulen speichern kann. Nur wie viel ist viel und wie stellt man es sicher, dass immer mindestens 20 kV an den Kerzenelektroden anliegen?

Zu dem „wie viel“ half mir dann auch das oben erwähnte „Handbuch Verbrennungsmotor“ weiter, hierin steht sinngemäß:

"Homogene stöchiometrisch Kraftstoff-Luft-Gemische benötigen ruhend für die Entflammung eine Energie von weniger als 1 mJ. In fetteren oder abgemagerten Gemischen erhöht sich der Energiebedarf dann auf 3 mJ. Im realen Motor steigt durch inhomogene Verteilung von Luft, Kraftstoff, zurückgeführtem Abgas etc. und durch Übertragungs- und Wärmeverluste an Zuleitungen und Elektroden der Energiebedarf jedoch erheblich an."

Wie viel dies dann sein sollte, wird jedoch leider nicht beschrieben und lediglich darauf verwiesen, dass derzeit moderne, konventionelle Zündsysteme ca. 40 mJ mit einer Funkendauer von 1 ms an den Elektroden zur Verfügung stellen können. Also sollten es dann 20 kV und 40 mJ werden, mit welchem ich hoffte, mein Problem mit der Viertakterei zu erledigen. Um diese Werte zu erreichen, erschein es mir dann damals am einfachsten, die herkömmlichen Zündspulen durch sogenannte "Hochleistungs"-Spulen zu ersetzen.

Dazu vielleicht mal kurz zur Erklärung:

Eine Zündspule arbeitet wie ein Funkeninduktor. Bei eingeschalteter Zündung –also geschlossenem Unterbrecher- wird die Primärwicklung der Zündspule von Strom durchflossen, wodurch sich ein Magnetfeld um die Spule bildet. Dieses Magnetfeld wird durch den gemeinsamen Eisenkern beider Wicklungen auch auf die Sekundärwicklung übertragen. Das Öffnen des Unterbrechers im Primärkreis der Zündspule lässt dann das aufgebaute Magnetfeld schnell zusammenbrechen, wobei im Sekundärkreis ein Hochspannungsimpuls induziert wird. Diese Hochspannung gelangt dann durch das Zündkabel zur Funkenstrecke einer Zündkerze, um hier dann das Kraftstoff-Luft-Gemisch zum richtigen Zeitpunkt zu entzünden.

Im Detail, aber auch nur grob umrissen, funktioniert das Ganze dann so:

Beim Einschalten (z.B. dem Schließen der Unterbrecher) eines Gleichstromkreises mit einer Spule verhindert die der Betriebsspannung entgegenwirkende Induktionsspannung (siehe Lenzsche Regel) einen raschen Stromanstieg, wobei der Anstieg dann den Regeln einer e-Funktion {I(t) = Io * ( 1 - exp( - t / tau))} folgt (bei einer idealen Spule mit der Induktivität 1 H und einer Spannung von 1 V ist der Strom nach 1 s auf 1 A angewachsen). Der Anstieg des Stroms wird sodann im Laufe der Zeit immer geringer, wobei rein physikalisch gesehen der maximale Strom in der Unendlichkeit, also nie erreicht wird (in der Technik gibt man sich – meine ich - mit 0,9 des Maximums zufrieden).

„Aufgemalt“ sieht dann das Ganze z.B. bei einer realen Zündspule (Pertronix Flame Thrower) so aus:

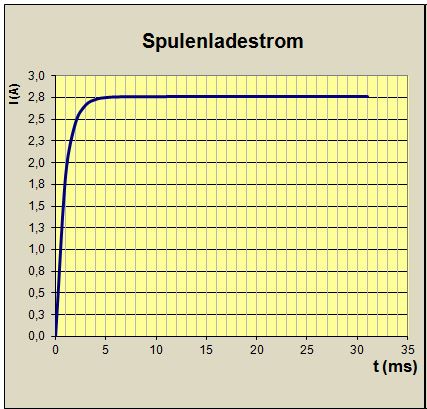
Wie man sieht, hat die Pertronix-Spule den Zustand des annähernd maximalen Stromanstiegs nach ca. 25 ms erreicht. Die Wartburgspule braucht hierfür dagegen lediglich 5 ms:

 

Am Punkt des maximalen Stromanstiegs ist sodann der Kern der Spule nahezu gesättigt und die Spule hat eine bestimmte Menge an Energie gespeichert. Passend zu den oben gezeigten Stromanstiegskurven die maximal erreich- und speicherbare Energie der Pertronix Flame Thrower:

 

und der FER Kleinzündspule:

Wie man sieht, erreicht man mit der Pertronix-Spule den ca. 7,5 fachen Wert der Wartburgspule (123,91 mJ vs. 16,59 mJ).

Das „Schöne“ daran ist, dass die maximal speicherbare Energie hierbei vor allem von der Induktivität der Spule bestimmt wird – und diese Wiederrum von der Anzahl der Drahtwindungen und der Größe und Bauart des Spulenkerns. Eine Zündspule, welche mehr Energie speichern kann, muss daher per se größer ausfallen, es sei denn, der Hersteller hätte hauptsächlich Luft ins Gehäuse eingebaut.

Beim Abschalten (Öffnen des Unterbrechers) wird sodann die in die Primärspule gespeicherte Energie auf die Sekundärspule übertragen. Dies erfolgt durch das Zusammenbrechen des Magnetfelds der Primärspule welches nicht nur in der Primärspule eine hohe Gegeninduktion zur Folge hat (zwischen 200 und 500V stehen dann an der Klemme 1 der Zündspule an) sondern auch in der Sekundärspule eine Spannung induziert, deren Höhe zur Hauptsache vom „Übersetzungsverhältnis“, daher dem Verhältnis der Windungszahlen der Primär- zur Sekundärspule abhängt und einige KV erreicht (übrigens im – Bereich). Auch hier mal die Unterschiede zwischen der Pertronix und der FER-Spule:

Pertronix

FER

Diese Spannung im kV-Bereich steht sodann übertragen über das Zündkabel, den Kerzenstecker und die Kerze auch an den Elektroden der Zündkerze an und sorgt hier dafür, dass sich das Gas zwischen den Elektroden ionisiert und damit elektrisch leitfähig wird. Ist dieser Zustand erreicht, kommt es zum Stromfluß über das ionisierte Gas und es bildet sich ein „Plasmakanal“ mit hoher Temperatur (durch die hohe Energiedichte des großen Stroms) aus, welchen wir alle als „Zündfunken“ kennen.

Nun entlädt sich die Zündspule allerdings ebenso wenig schlagartig, wie sich dies schlagartig auflädt, denn auch auf der Sekundärseite entsteht eine entgegenwirkende Induktionsspannung, welche den Entladungsstrom begrenzt. Die physikalischen Verhältnisse sind hierbei etwas anders gelagert, führen aber durch die entstehende Selbstbegrenzung dazu, dass sich die Nachbrennphase, bzw. Glimmentladung einstellt. Dies hält so lange an, wie die Spannung an den Kerzenelektroden so hoch ist (ca. 1 kV), dass sich der oben erwähnte Plasmakanal erhalten kann. Bricht dieser sodann zusammen, ist es mit dem „Zündfunken“ vorbei.

Hier schließt sich dann der Kreis zu den eingangs erwähnten Ausführungen von Richard van Basshuysen und Fred Schäfer und dem Paschen-Gesetz. Eine größere, leistungsfähigere Zündspule ist durch die höhere Sekundärspannung besser in der Lage, unter schwierigen Verhältnissen im Brennraum einen Plasmakanal, daher Zündfunken auszubilden und durch die größere Menge an gespeicherter Energie diesen Zündfunken auch länger aufrecht zu erhalten.

Da aber nun leider, leider beim Betrieb im KFZ die theoretisch maximale Aufladung der Zündspule durch die von der Drehzahl und dem Schließwinkel des Unterbrechers begrenzte „Ladezeit“ nicht erreicht wird, ich aber nun wissen wollte, was mich dann tatsächlich an "Leistungszuwachs" durch die Hochleistungszündspulen erwartet; und weil die Berechnung der von einer Zündspule gelieferten Werte kein Hexenwerk ist, habe ich mir hierfür ein Excel-Sheet gebastelt, gleich ein paar Diagramme zur "Visualisierung" etwaiger Änderungen der Ergebnisse über die Zeit und/oder die Drehzahl eingefügt und zuerst einmal mit der originalen Wartburgspule gerechnet:

Einmal zur Erläuterung – um die von einer Zündspule gespeicherte Energie und die Höhe der erzeugten Sekundärspannung halbwegs genau berechnen zu können, brauchen von dieser eigentlich nur drei Werte bekannt sein: der ohmsche Primärwiderstand, die Primärinduktivität und das Übersetzungsverhältnis der Primär- zur Sekundärspule. Leider hapert es aber meist daran; diese Angaben sind so gut wie nirgends zu finden, allenfalls der Primärwiderstand wird des Öfteren angegeben. Mir ist jedenfalls nicht gelungen, für mehr als eine Handvoll von Spulen diese Angaben zu erhalten. Hier einmal die originale blaue Bosch-Spule:

Weitere wichtige Angaben zur Berechnung sind natürlich die Versorgungsspannung direkt an der Zündspule (ich bin hier einmal von der Unterbrecherzündung ausgegangen, diese hat so gut wie keinen Spannungsfall über den Kontakten), der Schließwinkel, welcher ja in Abhängigkeit von der Drehzahl die mögliche Ladezeit der Spule bestimmt, sowie die Geschwindigkeit der Abschaltung des Primärstroms (hier als Öffnungszeit Unterbrecher bezeichnet). Die Öffnungszeit hat frappierende Auswirkung auf die Höhe der induzierten Primär- und damit auch der Sekundärspannung, und ich habe diese einmal fix auf glaubhafte 0,1ms festgelegt (dass diese sich über den gesamten Drehzahlbereich nicht wesentlich ändert, dafür sorgt übrigens bei der Unterbrecherzündung der Zündkondensator). Damit ergeben sich jedenfalls die Werte für die induzierte Primärspannung, welche üblicher Weise in den Datenblättern der Spulen auch immer so angegeben werden (von ca. 200V bei einer Standardspule bis zu ca. 500V bei eine Hochleistungsspule – siehe weiter oben), für einen praxistauglichen Vergleich verschiedener Spulen ist dies so genügend. Hier mal das Eingabefeld und die ausgegebenen Ergebnisse der Berechnung am Beispiel der Wartburgspule:

 

Weiterhin etwas idealisiert ist die Berechnung der Höhe der Sekundärspannung, da hier der Einfachheit halber alle Übertragungsverluste ausgeklammert sind. In der Praxis wären je nach Wirkungsgrad der Spulen vielleicht 2% bis 5% abzuziehen, aber für einen größenordnungsmäßigen Vergleich ist dies auch ohne diesen Abzug ausreichend.
Auf diese Art und Weise war es dann recht einfach, die Zündspulen, von welchen ich Daten erhalten hatte, miteinander zu vergleichen, dies eben auch unter Berücksichtigung der Aufladezeitbegrenzung durch Drehzahl und Schließwinkel. Hier einmal die Zusammenfassung:

 

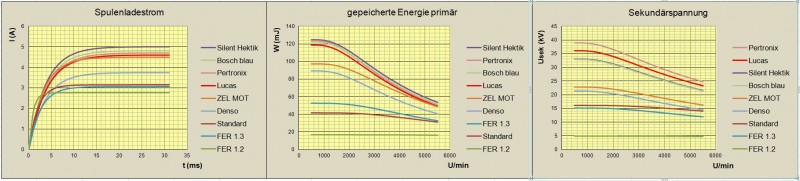
Wie man leicht erkennt, sind die als Hochleistungsspulen beworbenen tatsächlich solche, die Leistungsdaten der Spulen liegen dicht beieinander. So schaffen es die Silent-Hektik, die Pertronix, die Bosch und die Lucas beim AWE-Motor mit 130 Grd. Schließwinkel noch bei 5500 U/min über 40 mJ zu speichern und über 20 kV bereit zu stellen. Die ZelMot-Spule ist übrigens polnischen Ursprungs und war auch in der DDR verfügbar, richtig schlecht ist diese auch nicht. Bei der Denso-Spule handelt es dann nicht um eine der üblichen Becherspulen, diese hat eine moderne Kompaktbauform und ist recht klein. Beide Spulen schaffen noch die 40 mJ Grenze, aber nicht mehr die 20 kV. Der Rest der Spulen ist gegenüber den Hochleistungsspulen weit abgeschlagen.

Auf Grund der Erkenntnis, dass die Hochleistungsspulen bzgl. ihre Leistungsdaten tatsächlich alle so dicht beieinander liegen, fiel mir dann die Entscheidung, welche Spule ich verwenden werde, recht leicht. Über den Preis bin ich da zu der Beru ZS106 gekommen, welche ich alle drei zum Preis einer einzigen blauen Boschspule erwerben konnte. Mit der Entscheidung bin ich jedenfalls sehr zufrieden, seit der Verwendung dieser Spulen waren dann auch meine Viertakterei-Probleme Geschichte.

An sonst gibt es natürlich auch noch weitere Hochleistungsspulen, welche die Werte der von mir betrachteten Spulen noch beträchtlich übertreffen. Allerdings übersteigt dann bei diesen der Primärstrom den für die Unterbrecherzündung geltenden Nennstrom von 5 A (hierauf hatten sich die Hersteller mal irgendwann früher geeinigt) bei weitem, großer Kontaktabbrand und dadurch eine verringerte Lebensdauer der Unterbrecher wären dann die Folge. Bei der Verwendung von elektronischen Zündungen muss man aber sowieso schauen, welchen Strom diese auf Dauer schalten können. Da einem dies aber kaum mitgeteilt wird, bzw. Daten nicht vorhanden sind, hatte ich mich dann für die Laubtech-Zündung entschieden, da der Hersteller hier 7 A als Nennstrom angibt, diese reichen vollkommen aus.

So, mehr fällt mir im Moment zu den Zündspulen nicht mehr ein, wer noch Fragen hat, bitte fragen, vielleicht kann ich diese ja beantworten.

-

« vorige Seite|Seitenanfang|